Dynamic Programming with Memoization

This is really as much for me as it is for anyone who reads this. If you want to really understand something, you must be able to teach it to someone else. I believe it. Thanks, Alvin at Structy for such a great and thorough breakdown.

Problem

    Return the nth value in the Fibonacci Sequence. 
    n will be passed in as input. 
    Fibonacci values are the sum of the 2 numbers before it.
    input: n --> an integer
    output: n --> an integer

Solution

Brute Force Solution

    def fibonacci(n):
        if n == 0 or n == 1:
            return 0
        if n == 2:
            return 1
        return fibonacci(n - 2) + fibonacci(n - 1)

    print(fibonacci(5))

Optimized Solution

    def fibonacci(n):
        return _fibonacci(n, {})

    def _fibonacci(n, memo):
        if n == 0 or n == 1:
            return 0
        if n == 2:
            return 1
        if  n in memo:
            return memo[n]

        memo[n] = _fibonacci(n - 2, memo) + _fibonacci(n - 1, memo)
        return memo[n]

    print(fibonacci(35))

The Steps to Dynamic Programming Success

1. Draw and Visualize the Problem As A Tree

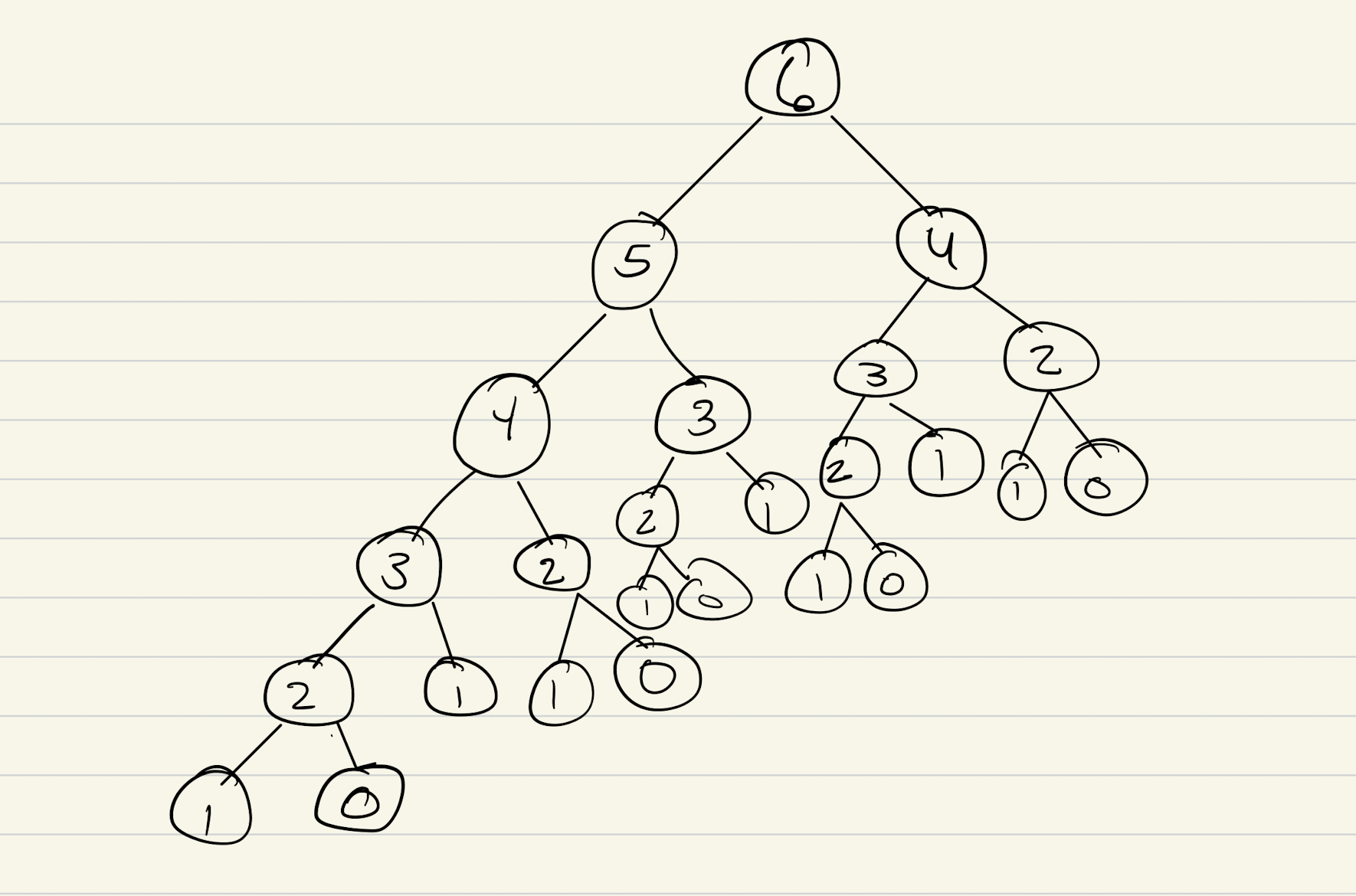
2. Find The Base Case In The Tree

In our case, the base case will be: - When the input value is a 1 or 0. 0 and 1 can't be broken down any further.

So, anywhere you see a 0 or 1 node value, highlight it as that will tip us off that we have reached a base case.

3. Move to the bigger problems that haven't yet been solved

So we've solved fib(0) and fib(1). The goal is to solve fib(6), so we have a few more solutions to find before we are finished. fib(2) is next up for solving.

Note: What is the recursive call returning?

As you walk through your code, you must be confident in determining what the recursive call is returning. Stay aware of the sub-results. If you haven't yet made it to the top of the tree and your return value is wrong, there is a problem somewhere with a calculation.**

4. Calculate the sum of the children of your next value

2's children == 1 and 0, giving fib(2) a return value of 1.

5. Repeat Number 4 Until You Reach the Bottom of The Stack

With fib(2), we will continue to fib(3), repeating 4 until we have made it to the bottom of the call stack.

6. Analyze the Time and Space Complexity

1. Time Complexity of this problem? (Brute Force) - Each node in the tree equals 1 recursive call, meaning however many recursive calls we have to make should be reflected in the complexity. Ask yourself, how many nodes are on each level of this tree? - You'll notice that the number of nodes increases by double as you go down a level. So, we have a 2 thus far...Now consider the total number of levels, which as discussed is determined by the input. The number of levels will be fibonacci(n) --> In our case n is 6 for the first test case. Giving us an initial Time Complexity of O(2^n) - Exponential.

2. Space Complexity of the problem? - Space complexity will be highly dependent on number of (call)stack frames that we use for our recursion. Remember, whenever you make a recursive call, that information has to be stored on the (call) stack until it returns. To make this clearer, let's visualize the call stack as we break this problem down.

3. What's the Optimized Time/Space Complexity When Adding In Memoization? - This knocks our time to O(n) and space O(n). Space is simply gonna be the height/# of levels in our tree, which is depending on the input

Visualizing The Call Stack

So we start with the input being loaded on the stack. The recursive call is made and the child is added to the top of the stack. Recognize that every time we make a recursive call, we're adding a new stack frame, and you're only able to remove a stack frame when it returns. Once we reach a base case, in our case, 1 being on the top the 1 value is popped off, so we now have to look at 2's right child since it's the next value up on the stack.

Using a recursive approach, which utilizes the call stack under the hood tells me that we are using the Depth First Approach to fibonacci. Depth First meaning go deep as far as the tree can take us before traversing diagonally.

DFS Traversal Flow

Visual Addition of Values to the Call Stack

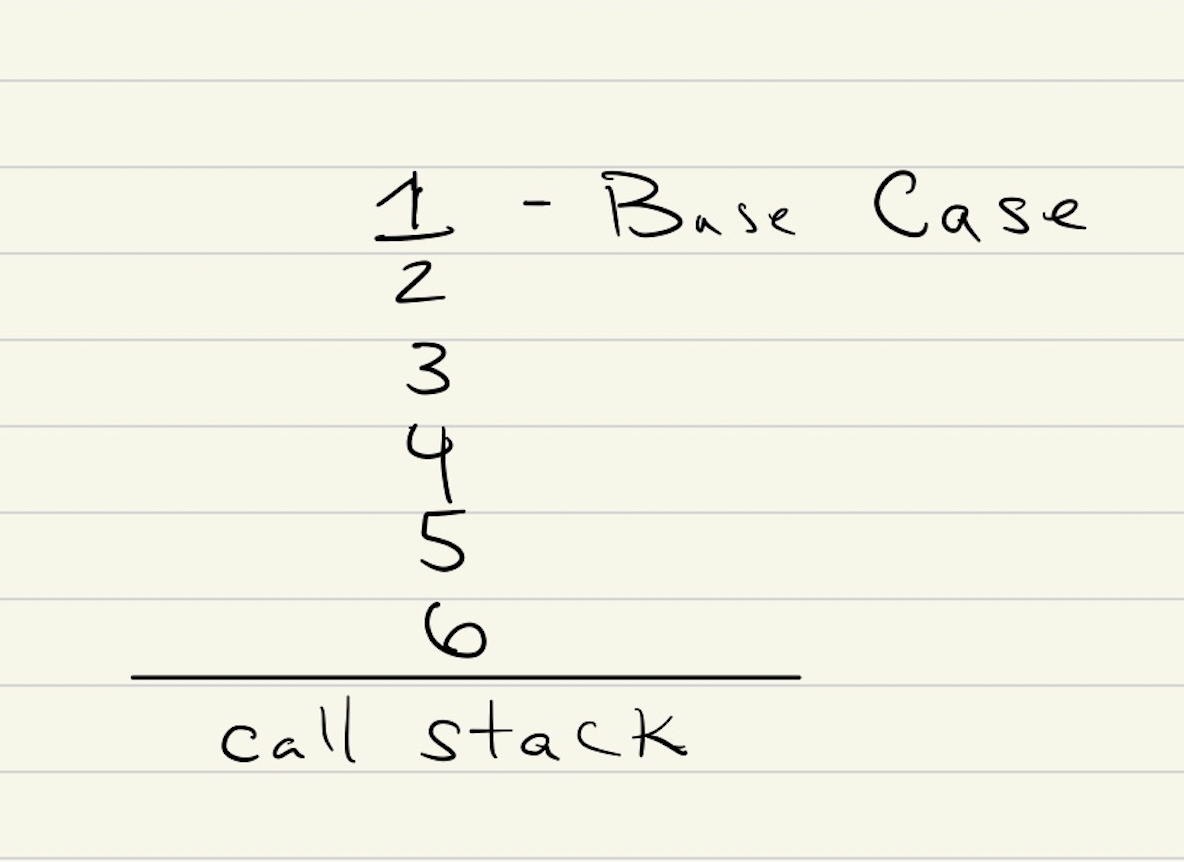
Steps

Visit & Add 6 to Call Stack

Visit & Add 5 to Call Stack

Visit & Add 4 to Call Stack

Visit & Add 3 to Call Stack

Visit & Add 2 to Call Stack

Visit & Add 1 to Call Stack

Making Our Way to the bottom of the call stack fib(6)

2 --> Visit Right Child, 0 --> fib(2) returned

3 --> Visit Right Child, 1 --> fib(3) returned

4 --> Visit Right Child, 2 --> fib(4) returned

5 --> Visit Right Child, 3 --> fib(5) returned

6 --> Visit Right Child, 4 --> fib(6) returned

Our base cases have been reached and return a value, fib(1) and fib(0). We can now make our way back up to fib(6)

fib(2)

2 --> Left Child of 2 Has Already Been Visited Calculated(DFS), so visit the right child, 0. Once we have 0 calculated, we can combine the left and right child of 2 to get the answer for it's parent, fibonacci(2). The 2nd fibonacci value equals 1, 1(left) + 0(right). With fib(0), fib(1), and fib(2) answered, we are now on our way back up the tree. Next node value up is 3.

fib(3)

3 --> Left Child(2) has already been visited and calculated, move to the Right Child of 3 --> 1 --> 1 is a base case so we have a return value --> Left Child fib(2), and Right Child fib(1) give us our answer to fib(3), 2. Let's continue our traversal back to the bottom of the stack, fib(6)

fib(4)

Looking at the children of 4, it's left child,fib(3) has already been visited and returned. We only have to visit the right child, fib(2). Well, 2 has already returned as well so the only left to do is combine the return values of fib(3) and fib(2) to get fib(4). fib(4) comes out to be 3.

fib(5)

With fib(4) solved, returned and off of the stack, we only have 2 values remaining to calculate, fib(5) and fib(6). As with the other values earlier, the left child, fib(4) has already returned and been solved. Let's move to the right child, fib(3). It has already been solved as well. We can speed it up at this point. fib(5) is the sum of fib(4) and fib(3), 5.

fib(6)

We've made our way to the bottom of the call stack frames. Everything needed to solve for fib(6) is there for us. fib(5) plus fib(4) give us our answer, 8.

We've already looked at the left child which was the initial node on top of the stack, now we need to make a recursive call to right child, placing it on the stack above 2. We're done with both of 2's recursive calls (to 1 and 0) at this point, so it can safely be removed from the stack, moving to the value below it, 3. We've checked the left child of 3 already. DFS is deep as you can go before moving horizontally. Next node to check is the right child of 3, another 2, placing it back on the stack.

At most, you're gonna have the number of levels on the stack. If the levels(input) is 4, you'll have 4 at most. All of them aren't stored simultaneously. To add stack frames, you must have returned from other ones. This leads to space complexity being O(n), with n being the input/total number of tree levels.

So, how do we optimize? Exponential/ O(2^n) isn't great and will fail with a larger number

With time being O(2^n), that really isn't good enough as the inputs become large. This is where optimizing the solution comes in. This is where you really understand what the tree actually represents. Every node in the tree represents a problem. Same value multiple times in the tree? That means you have duplicates. Surely you could cut down some time if you ignore duplicates that have been seen before.

4 is seen twice in the tree. Once we've solved it (and the children of it) once, its answer should be saved somewhere since duplicate nodes are essentially solving the same problem. So, if we store the sub-results, we benefit by not having to make the same calculation again. What we need to do is prune/remove the duplicate subtrees(except the parent of the subtree). This strategy is called MEMOIZATION.

With Python, we use a Dictionary, since it gives us a O(1) Lookup time for finding n(the value). Everything prior to memoizing the problem remains, we are just incorporating memoization into it now. Once we have our first returned recursive call, meaning the base case has been met, we will add the input as a key and it's sum/the return value as the value to the memo dictionary.

So, we'll always have a reminder and can look in the memo to not forget the the 2nd fibonacci number is 1. With another value returned from the call stack and popped off we now have a new n to analyze. This is where things get interesting...

The Benefit of Memoization in Dynamic Programming

We're on 4 at this point. It's children are 3 and 2. 3 is already returned as well as 2. If you look at the memo, we realize that we've already gotten the value for both, meaning, we won't have to make another recursive call for the right child of 2 since it was done prior when calculating the left child. It fetches the value, combines it with the other child and we're able to return what the 4th fibonacci (fib(4)) is.

Saving the value of the Recursive Call

We can't forget to store the value of fib(4). You saw how much less work we had to do since 3 and 2 were stored? Keep at it with fib(5) and fib(6). We get the answer, and we get it much quicker with memoization. Where you may only pass 5 test cases initially and fail all larger numbers, you'll now be able to pass them all with memoization added to your tool belt.

To ensure you understand the problem, I would solve it firstly without memoization. Once those test cases begin to slow down and fail, this is the point where memoization will come in handy.